昔書いた以下の続き、発展の話
上記で
発展的課題としては、どうにかしてDoubleの精度ギリギリまで全部計算するとか、コンパイル時に使える有理数やBigIntを1から作って、さらにDoubleの上を目指す、などしてみると楽しいでしょう(?)
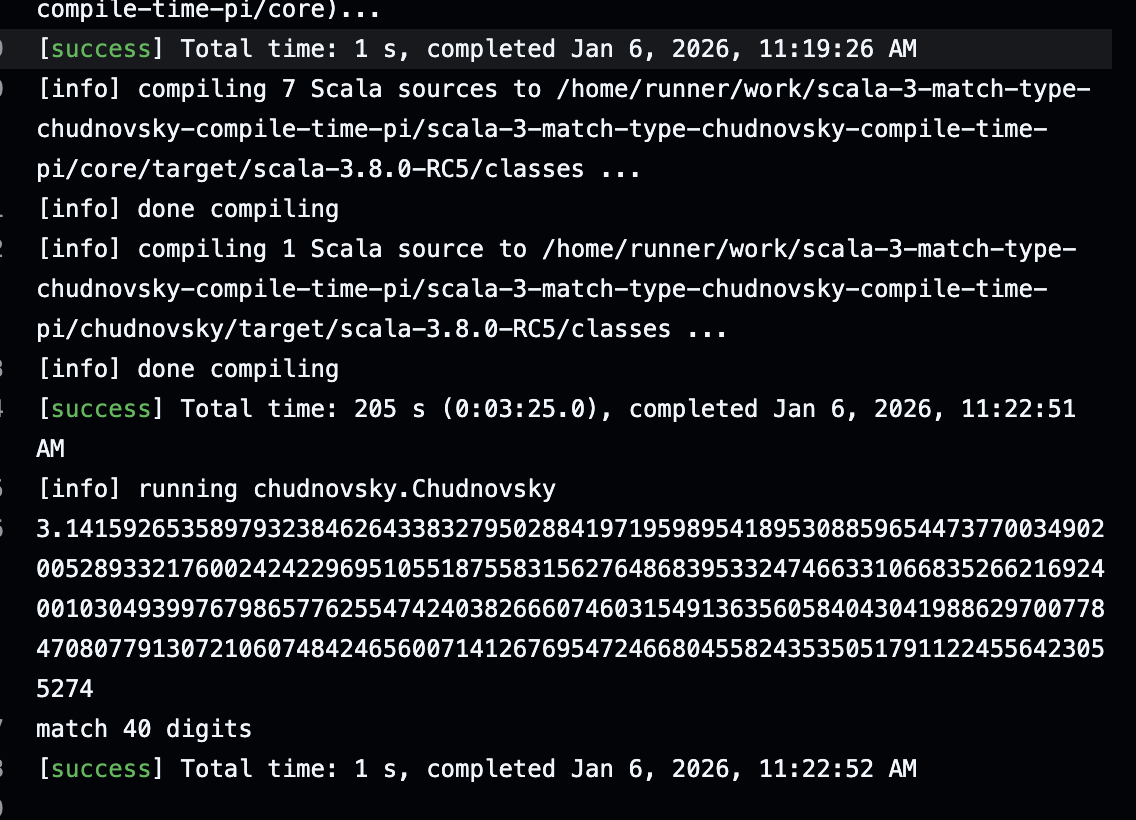
と書いてましたが、それをやりました。scala.Doubleの精度超えました。やったー。
40桁という数値だけ見ると、なんかあまりインパクトないですが、思ったより大変で辛いです。
これを大幅に超える挑戦者を募集しています(?)
コードは以下です
本来は円周率関係ない部分も「compile time数値ライブラリ」を目指して(?)もっと色々やっていたのですが、ある程度必要な部分だけ切り出しました。
ズルしてる部分や、実装詳細のポイントとしては
- unsigned int(自然数)、signed int(整数)、unsigned rational(符号なしの有理数)、signed rational(符号あり有理数)、などを割と真面目に実装
- unsigned intは、Scala 3標準を使わずに、独自に型レベルな2進数Listとして実装
- Scala標準のLongやDoubleを超える範囲を扱うにはそうするしかないはず
- このあたりを読もう
- https://gist.github.com/sile/50f6f7f98b71ab3e421d
- https://github.com/harrah/up これ割と参考にというか、可能な部分は直訳した。Scala 2での同等なtype level programming
- https://apocalisp.wordpress.com/2010/06/08/type-level-programming-in-scala/
- "purely functional data structures" と "dense" などでググろう
- 高速な真面目な割り算が辛いので、途中での割り算や剰余や約分の計算をできるだけ後回しにし、最終的な約分や割り算や10進表示のための変換をcompile時にやってない、というだいぶズルをした!!!
- とはいえ有理数同士の足し算は明らかに必要なので、分母を揃えるための通分はするのだけど、分母揃えるのに「雑に掛け算してしまう」か「しっかり最小公倍数を計算する」か、実装の手間と速度を天秤にかけて、どちらにするか?的な観点
- 高速な割り算だけでも、突き詰めると記事を何個でも書けるとか、論文書けるレベルなので
- そこもガチ勢じゃないので説明できませんが、例えばこういうの https://qiita.com/square1001/items/1aa12e04934b6e749962
- 「有理数を任意桁数の10進表記小数へ高速に変換」が一番辛そうな気がしたけど、そもそもあまり真面目に挑んでないから難易度が不明
- すごく効率悪そうな実装や、Scala 3の標準に頼る実装(つまりそれはDoubleの精度までになる)、なら可能だったが
- ルートの計算も真面目かつ汎用的なものの高速実装は辛そうなので、ルートを計算する数値は事前にわかっていて固定なので、連分数展開で計算した
- 連分数展開での計算が本当にコスパいいのか?は謎
- 多少無駄な部分ありそうだけど、Scalaファイルだけで860行もある・・・
- debug print的なものが一切不可能なので、どこが遅いのか?を計測するのがほとんど不可能なので、それがとにかく辛い
- 誰か方法思いついたら教えてくれ〜〜〜
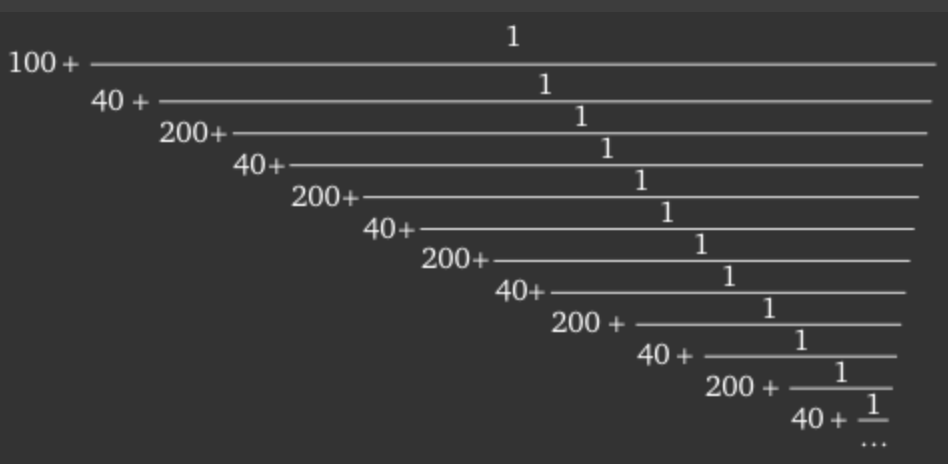
chudnovskyについて
- 数学ガチ勢ではないので詳しい説明は出来ないンゴ
- https://en.wikipedia.org/wiki/Chudnovsky_algorithm
- ググるかAIに聞いて
- ラマヌジャンの式の発展系で、実際に今も世界記録出すのに使う式なの?(よく知らん)
- 1つ増やすごとに14桁くらい精度上がるらしい、すごい(π計算初心者の感想)
- 40桁ということは、つまり2までしか入れてません
- 自分の現状の実装では、指数的なオーダー(詳細不明)でcompile時間が増減するので、3とか4入れたら、数十分や数時間かかりそう、あるいはcompilerが途中で死にそうなので、試してない
- 追記: 3を試したけど2時間経過しても終わらなかった
- ここ https://www.craig-wood.com/nick/articles/pi-chudnovsky/ 参考にして、ルートを外に出して、本来のよく見る形と微妙に違う表現で計算
よく見る形↓
(分母に"2分の3乗"がいて辛い)
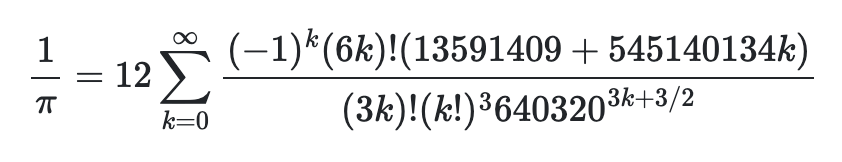
利用した形↓
(ルートの計算が10005に対して1回だけになって嬉しい)
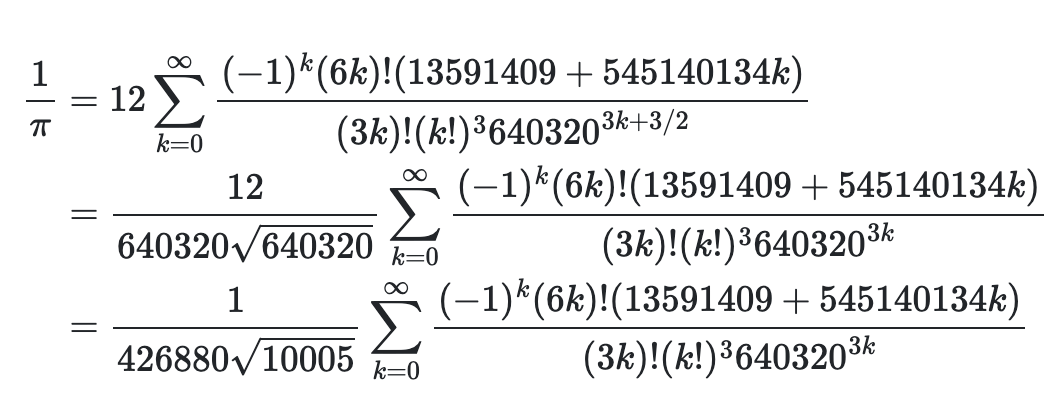
(元記事にはさらに色々書いてあったけど、その後の部分は読んでない、利用してない)
compileにはGitHub Actions上で3分越え
(1回しか計測してないので、余計な部分もあるはずなので、正確な時間は不明)